Sección Áurea

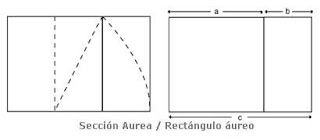
Es la división armónica de una recta en media y extrema razón. Esto hace referencia, a que el segmento menor, es al segmento mayor, como este es a la totalidad de la recta. O cortar una línea en dos partes desiguales de manera que el segmento mayor sea a toda la línea, como el menor es al mayor. De esta forma se establece una relación de tamaños con la misma proporcionalidad entre el todo dividido en mayor y menor, esto es un resultado similar a la media y extrema razón. Esta proporción o forma de seleccionar proporcionalmente una línea se llama proporción áurea, se adopta como símbolo de la sección áurea (Æ ), y la representación en números de esta relación de tamaños se llama número de oro = 1,618.

 El mejor ejemplo de esta relación lo podemos observar en la Gioconda. Las obras de Leonardo Da Vinci se fijaban sobre un rectángulo basado en la proporción aurea, en la Gioconda, el rostro encaja dentro de un rectángulo áureo, cada parte de la cara se componen a su vez en rectángulos o proporciones áureas.

Otro gran ejemplo con una disposición distinta de las proporciones áureas la podemos observar en su obra El hombre de Vitruvio .



Lo largo de la historia de las artes visuales, han surgido diferentes teorías sobre la composición. Platón decía: es imposible combinar bien dos cosas sin una tercera, hace falta una relación entre ellas que los ensamble, la mejor ligazón para esta relación es el todo. La suma de las partes como todo es la más perfecta relación de proporción.

Su Utilidad es:

·         Buscar la armonía entre las formas donde cada crecimiento o decrecimiento de la figura es basado en una proporción que hace que la figura tenga un orden determinado.

·         Con dicha proporción  se puede generar todo tipo de figuras, estructuras, cuadros, objetos porque de cierta manera organiza y divide el espacio de manera que todo siga un mismo patrón y los resultados sean objetos perfectamente proporcionales.

·         La proporción aurea permite generar modelos exactos a la realidad y así poder en la simulación ver el comportamiento del sistema



Fuentes: 

-http://www.artesaniasymanualidades.com/tecnicas/la-seccion-aurea-aplicada-al-arte.php
-http://www.tuobra.unam.mx/obrasPDF/publicadas/050713181602.html
-Imágenes extraídas de Google